Estamos no Ar...
Potencias com expoente racional
O conjunto dos números racionais é formado por todos os números que podem ser escritos na forma m/n , onde m é um número inteiro qualquer e n um número inteiro qualquer diferente de zero. É indicado pela letra maiúscula Q, e representado da seguinte forma:

Vejamos alguns exemplos:

Do mesmo modo anterior, preservando a propriedade fundamental, e fazendo p = m/n, teremos:

Vejamos exemplos da definição acima:
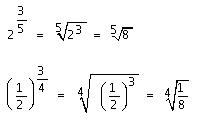
Potencias com expoente racional
O conjunto dos números racionais é formado por todos os números que podem ser escritos na forma m/n , onde m é um número inteiro qualquer e n um número inteiro qualquer diferente de zero. É indicado pela letra maiúscula Q, e representado da seguinte forma:
Q = {x | x = m/n, m ∈ Z , n ∈Z*}
De modo geral, baseando-se na propriedade fundamental, temos: ap .aq = ap+q , deste modo, fazendo p = 1/n , teremos :

Vejamos alguns exemplos:

Do mesmo modo anterior, preservando a propriedade fundamental, e fazendo p = m/n, teremos:

Vejamos exemplos da definição acima:
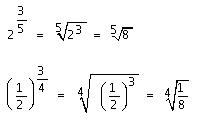


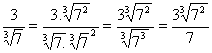
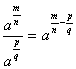
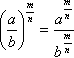
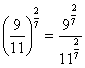



 sendo a um número real;
sendo a um número real; com a um número real.
com a um número real.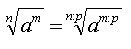

 1. Essas propriedades permitem simplificar certos radicais, tirando fatores do radicando.
1. Essas propriedades permitem simplificar certos radicais, tirando fatores do radicando.